Code and Tools

Tempus adipiscing commodo ut aliquam blandit

Hands-on tutorial: Granulometric analysis of 21 cm tomography

This is a hands-on tutorial on the granulometric analysis of 21 cm tomographic data (image or datacube). In-depth discussion about the astrophysical application is described in Kakiichi et al. (2017) (https://arxiv.org/abs/1702.02520). This tutorial aims at describing the practical aspects and the python script of the method.

Background: algebra of shapes

First of all, we need to set up a mathematical tool: algebra of shapes. The followings are the well-defined operations in mathematical morphology[1,2,3].

The Minkowski addition (dilation) is given by the union of a binary field, X, and a structuring element, S, as the structuring element is moved on the binary field. The diagram below illustrates how this Minkowski sum operation works.

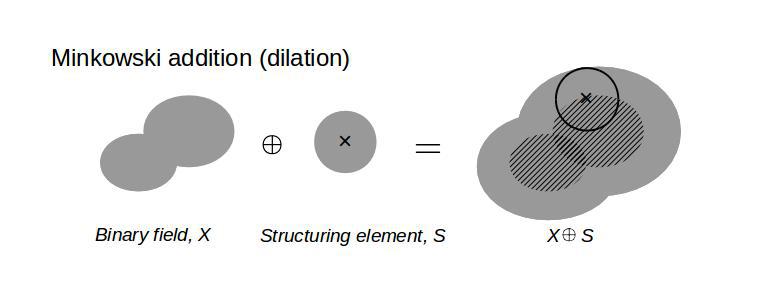
Figure 1. A schematic illustration of the Minkowski addition. The resulting image is shown as the grey area. The shaded region indicates the original image before the operation.

The Minkowski subtraction (erosion) is given by the intersection of a binary field, X, with the centre of a structuring element, S, as the structuring element moves on the binary field. The diagram below illustrates how this Minkowski subtraction operation works.

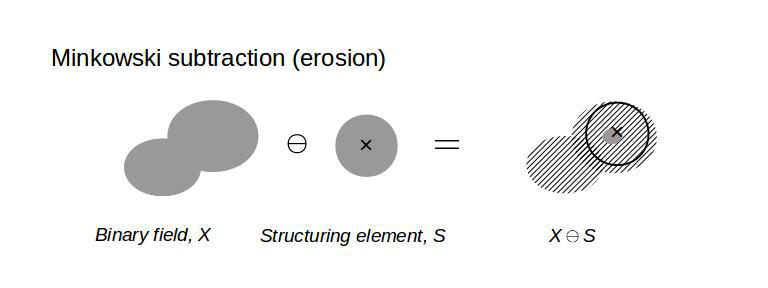
Figure 2. Minkowski subtraction. The colour coding is same as Figure 1.

The morphological opening is defined by a consecutive operation: Minkowski subtraction followed by Minkowski addition.

Figure 3. Morphological opening. The colour coding is same as Figure 1.

The morphological opening can be used as a mathematical abstraction of the concept of sieving. This concept of sieving is the central idea behind the granulometric analysis of images.

Reference

add reference and useful further readings

Neque ornare adipiscing

Eget mi ac magna cep lobortis faucibus accumsan enim lacinia adipiscing metus urna adipiscing cep commodo id. Ac quis arcu amet. Arcu nascetur lorem adipiscing non faucibus odio nullam arcu lobortis. Aliquet ante feugiat. Turpis aliquet ac posuere volutpat lorem arcu aliquam lorem.